Локальный гомеостазис как управляемая система

Естественная технологическая система патологии
"Современная наука базируется на двух идеалах: внутреннем совершенстве и внешней обоснованности. В этом подходе есть уникальность, последовательность, стройность, он объединяет живое и неживое, он эволюционен и активен, основываясь на прошлом, он устремлен в будущее". Эти слова академика А.М.Уголева позволили преодолеть многолетнее противостояние естествознания и технологии. Бурное развитие естественных наук и биоматематики, исследования наиболее важных процессов в биологических системах, успехи производственных технологий, позволили интерпретировать ряд закономерностей, общих для искусственных технических и естественных технологий живой природы.

Физиология есть учение о явлениях живой природы и ее задачей является исследование жизненных процессов. Это приводит к представлению о технологиях в живых организмах как о науке, изучающей принципы, структуру и динамику их организации. Но если естественная технология есть наука об организованных процессах, то изучение естественных и искусственных технологий может идти с применением идентичных принципиальных подходов. Одним из них является моделирование на абстрактных условных образах, сходных в математическом отношении с изучаемым процессом и отражающем его.

Свойство гомеостазиса, которое в биологии связывают со стремлением некоторого технологического механизма биологической системы сохранять постоянство, направленное на поддержание жизнедеятельности на всех уровнях, присуще и искусственным техническим системам. Их принципы разрабатываются так, чтобы обеспечить надежность различными путями, главный из которых — придание системе собственных свойств сохранения при воздействии экстремальных возмущений. Понятие гомеостазиса — основополагающее понятие общей теории систем: потеря устойчивости управления, переход в неравновесное состояние, равносилен потере гомеостазического качества. Свойство гомеостазиса в технических системах управления обеспечивается созданием запасов устойчивости.

Феномен жизни проявляется в борьбе гомеостазических и антигомеостазических процессов. Локальный гомеостазис возникает в ходе формирования подмножеств клеток баланса эквивалентности и провоцируется ими, как процесс необратимого нарушения естественных технологических процессов сохранения гомеостазиса. Возникает понятие естественного технологического процесса злокачественной патологии и мы уже установили наличие некоторых принципов его организации. Но является ли такая организация управляемой и является ли процесс технологическим? Или это действительно хаотический "развал", гибель отношений гомеостазиса? И если управляемый процесс существует, то какими механизмами он управляется? Возникает множество вопросов, ответ на которые должен конкретизировать понимание отношений на множествах клеток возмущенной биологической структуры.

Мы рассматриваем специфические принципы процесса злокачественной патологии, как естественное проявление жизнедеятельности. Это позволяет изучать их с технологических позиций. И это порождает важный вопрос: не является ли технологический процесс роста опухоли отражением, результатом управления, направленного не только на создание, но и на необратимое удержание антагонистических изменений механизма гомеостазиса, этой важнейшей функции сохранения живого организма?

Организации топологического пространства локального гомеостазиса показывает, что оно, несмотря на то, что любое его множество открыто, не может рассматриваться как строго дискретное. Его подмножества не состоят только из изолированных точек и имеют накопления клеточных подмножеств различного характера. Эти накопления позволяют провести параллель между специфическими свойствами клеточных множеств и рядом свойств, присущих искусственным технологическим системам с сосредоточенными параметрами. Такое сопоставление позволяет более четко определить носитель, выявить место и роль целевой функции, стабилизирующей рост опухоли. Даже проведение качественных аналогий между системой локального гомеостазиса и дискретно-непрерывными системами управления объектом с сосредоточенными параметрами, показывает наличие определенной общности между ними. Так, накопление шаром локального гомеостазиса мощностей множеств озлокачествляемых клеток, отражает его свойство интегрировать множество всех изменений на множествах сетей выходов клеток пространств отправления из шара гомеостазиса и междушарового пространства, во множество всех входов пространств прибытия, покрываемых сферической поверхностью локального гомеостазиса. Феномен такого интегрирования отражается и в динамике трехкомпонентного роста. В искусственных технологических системах управления, интегрирующие звенья имеют широкое распространение.

Архитектура и генезис топологического пространства карциногенеза позволяют отнести локальный гомеостазис к классу систем управления, обладающих признаками многоканальных оптимальных систем регулирования. Законы оптимального регулирования присущи многим программным системам управления. Примером такой системы является система стабилизации движения центра масс носителя, выводящего на орбиту искусственный спутник земли и его углового положения в пространстве относительно центра масс.

Информация, содержащаяся на пересечениях пространственных фазовых решеток, позволяет оценить отображения отношений на ситуациях размножающихся клеточных множеств в терминах общей теории систем. Это открывает пути использования, для их изучения и оценки, инструмента искусственных технологий. Параметры фазовой траектории содержат оценки динамики трехкомпонентного роста как объекта управления. Это дает возможность проведения некоторой сопоставительной оценки отношений на сетях входа, изменения состояния и выхода локального гомеостазиса, как естественной технологической системы стабилизации движения, относительно искусственной технологической системы аналогичного назначения.

Если аналогии между отображениями отношений и характеристиками фазовой траектории локального гомеостазиса и траектории систем стабилизации движения в пространстве, будут найдены и оценены на показателях качества присущих системам управления движением, то это будет означать, что системе локального гомеостазиса, с позиций общей теории систем, свойственны особенности управляемой системы в классе программных систем обработки информации и исполнения, тем или иным образом организованных, целевых управляющих программ.

Одновременно это будет указывать на общность таких технологических систем, независимо от особенностей их происхождения, формы организации и физической структуры.

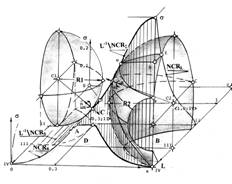
Архитектура топологического пространства. Архитектура топологического пространства и его подпространств в прямой проекции (на титульном рисунке в обратной), для наиболее типичного пересечения пространственных фазовых решеток показана на рисунке 1. Она отражает всю систему отношений роста в естественном технологическом процессе злокачественной патологии для этого пересечения. Обозначения указывают на фазовую траекторию — грань пересечений линейчатых поверхностей оболочек и на проекции фазовой траектории на координатные плоскости состояний S и L топологического пространства. A и B - области характеристической плоскости, покрываемые сферическими поверхностями гомеостазиса и локального гомеостазиса; C и D - области, покрываемые линейчатыми поверхностями пересечения фазовых решеток в междушаровом пространстве. Главным элементом архитектуры топологического пространства является фазовая траектория — исчерпывающая характеристика динамики процесса. Текущее время рассматривается как параметр фиксированного текущего состояния. Рассмотрим ее свойства как объекта общей теории систем, сопоставляя различные пересечения пространственных фазовых решеток.

Фазовые траектории в пространстве топологии.

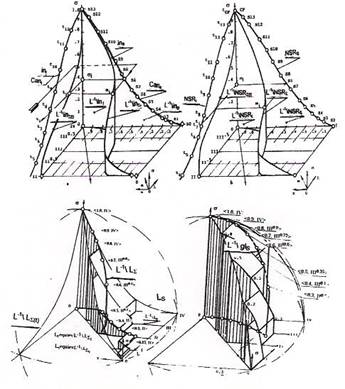На рисунке 2а, б сопоставлены фазовые траектории, в топологическом пространстве, для двух сагиттальных направлений роста, рассматриваемых ранее. Рисунок 2в отражает фазовую траекторию на самосопряженной решетке прозрачности ядер. На рисунке 2г приведена пространственная решетка и соответствующая ей фазовая траектория, иллюстрирующие результат интегрирования — накопления суммарного множества всех отображений изменений в перетоке. Эта решетка построена для gl-сагиттального представления, при котором агрессивность клеток возбуждающих и затягивающих подмножеств предполагается направленной одновременно по всем возможным, исходя из логики процесса роста, направлениям. Обозначения на рисунках соответствуют использованным ранее.

Из рисунков видно, что форма и параметры траектории определяют положение плоскостей гомеостазического переключения и раздела бигомеостазического пространства.

Площадные и объемные сечения бигомеостазического пространства для каждой из траекторий а, б, соотносятся между собой как 1:2. Это свидетельствует о различной активности клеточных множеств, охватываемых различными пересечениями решеток и о порождении, множествами клеток этих пересечений, первичных сетей выхода активируемых клеток с упреждением относительно различных направлений роста. Клеточные множества прибытия на этих сетях — множества всех отображений сетей выхода. Упреждение формирования первичных сетей выхода подтверждает лидирующую агрессивность клеток множества баланса эквивалентности на первичной сети входа, при разнице во времени гомеостазического переключения в 0.5 уровня.

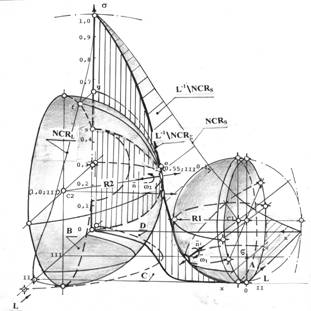
Специфическая системная роль фазовых траекторий в пространстве топологии, наглядно проявляется при рассмотрении образующих траектории геометрических мест точек в двух системах полярных координат, если принять в качестве их начала, соответственно центры шаров C1 гомеостазиса и C2 локального гомеостазиса.

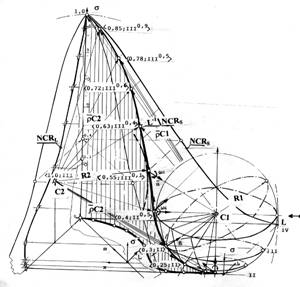
Проведем, на сагиттальном пересечении фазовых решеток (2б), из центров шаров гомеостазиса С1 и С2 встречные радиусы-векторы на след изображающей точки — фазовую траекторию (видны на рисунке 3) и проследим их синхронное и встречное, по направлению перемещения изображающей точки к фокусу, движение. Для этого спроектируем скольжение концов векторов вдоль траектории на основание x0L прямоугольной системы координат в единичном шаре. Множество проекций значений модулей векторов, отраженных на координатной плоскости x0L в единицах меры озлокачествления Гомпертца, а также их угловые параметры и параметры кручения, отражают и оценивают параметры взаимодействия ортогональных пространственных решеток, несущих фазовую траекторию. Обозначения аналогичны принятым ранее, цифры в треугольных скобках отражают координаты на плоскости x0L множеств клеток, соответствующих текущему положению изображающей точки при синхронном вращении концов проекций радиусов-векторов.

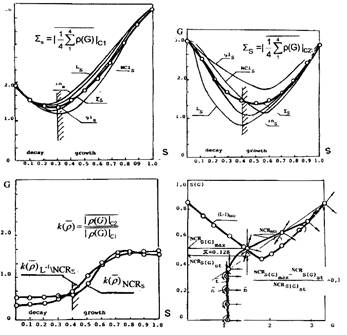На рисунках 4а,б приведены закономерности, отражающие изменения значений проекций модулей семейств радиусов-векторов по мере их скольжения вдоль фазовой траектории. Они отражают динамику состояний на сетях входа соответствующих пересечений (а следовательно и сагиттальных направлений роста), а также усредненное, по их множеству, значение изменений состояний, выраженные на мере озлокачествления G. Точки соответствуют вычисленным значениям.

Семейство значений модулей вектора системы гомеостазиса, проведенного из центра С1 (рис.4а), характеризуется ярко выраженным "компактным" минимумом в состоянии s, соответствующем значению единицы меры озлокачествления и равное, соответственно, значению радиуса шара гомеостазиса. Такая компактность отражает гомеостазический переход, близкий к одновременному, для всех сагиттальных представлений роста. Минимум, соответствующий скольжению радиуса-вектора, проведенного из центра локального гомеостазиса С2 для рассматриваемого семейства (рис. 4б), достигается на интервале их значений [0.4÷0,6] и доходит до величины близкой к значению 0.8 G с опережением в точке, приближенной на плоскости состояний, к началу роста growth.

Для различных сагиттальных представлений абсолютные минимальные значения проекций в случае сферической поверхности гомеостазиса, имеют различия, не превосходящие 0.25G, а для локального гомеостазиса они достигают значения, близкого к 1.0G. Можно предположить, что отмеченная разница в положении минимумов проекций этих радиусов-векторов, определяется изменениями на сети состояния биологического субстрата, соответствующими различиям в длительности удерживания изображающей точки на сферической поверхности локального гомеостазиса. С другой стороны можно полагать, что разброс положения этого минимума для множества проекций, связан с различием фактора агрессивности подмножеств клеток на сети входа, покрываемых различными сагиттальными оболочками, который в свою очередь зависит от мощности подмножеств клеток баланса эквивалентности, включенных в различные сагиттальные направления роста. По видимому, эти два фактора связаны друг с другом и удержание изображающей точки на поверхности шара локального гомеостазиса определяется характером агрессивности клеток баланса эквивалентности. Это ставит вопрос об оценке агрессивности множеств клеток состояния PROMOTION на первичной сети изменения состояния.

В этой связи можно полагать, что компактность положений минимумов, характерная для семейства радиусов-векторов, порожденных шаром гомеостазиса на сети входа, может свидетельствовать о равномощной начальной агрессивности множества клеток начальных фаз озлокачествления INITIATION, которые, тем не менее. уже приобрели тенденцию к дифференцировке по направлению роста. Такая дифференцировка становится заметной, начиная примерно с состояния s, незначительно превышающего отметку, идентифицируемую как 0.15 (константа нормального состояния). Об этом свидетельствует разброс положений значения минимума этих радиусов-векторов для различных сагиттальных направлений роста. Вместе с тем, это может отражать и порождение, на отдельных подмножествах клеток спокойного состояния, стартовых (под)подмножеств, покрываемых сферической поверхностью гомеостазиса и образующих первичные инициальные сети входа, а также первичные сети изменения состояния и выхода. Первичные сети коммуникационных взаимодействий трассируются, по-видимому, из нормального состояния.

Исполнительная функция системы локального гомеостазиса.

Усредненные по множеству E фазовых пространственных решеток средние значения проекций соответствующих модулей, можно рассматривать как усредненные отражения компонент фазовой траектории на плоскость состояний системы координат топологического пространства.

Так как шары гомеостазиса и локального гомеостазиса находятся в отношении транспорта озлокачествленных клеток из одного подмножества в другое и, одновременно, их (под)подмножеств из одной фазы состояния в другую фазу, упорядоченное множество параметров радиусов-векторов, проведенных из их центров на порождаемую их же взаимодействием фазовую траекторию, находятся в тех же отношениях. Эти отношения отражаются динамикой согласования перетоков и транспорта множеств клеток, покрываемых оболочкой топологического пространства, содержат информацию о динамике взаимодействия на сети изменения состояния в системе локального гомеостазиса и оцениваются алгебраическим отношением значений модулей радиусов-векторов.

Нас интересуют отношения проекций радиусов-векторов для множеств, отражающих текущее состояние биологического субстрата на плоскости x0G системы координат пространства топологии (сеть выхода). По мере развития процесса, в динамике роста, можно отобразить гипотетическую организацию динамических, непрерывно изменяющих состав и структуру первичных локальных сетей отображений входа, изменения состояния и выхода в окрестностях шаровой поверхности гомеостазиса, поверхности перетока и транспорта, в окрестности шара локального гомеостазиса. Структура, порожденная этими первичными сетями, конкатенирует множества всех текущих отображений входов, изменения состояния и выходов, объединяющихся в единую последовательную и динамическую систему с момента начала образования шара локального гомеостазиса и отраженную в завершенном состоянии, в полностью определенные древесную структуру и характеристическое поле канонизированного процесса. Отдельный интерес при этом, представляет вопрос о трассировке и организации первичных сетей маршрутизации стартовых множеств озлокачествляемых клеток из пластического состояния спокойного эпителия в гиперпластическое.

На рисунке 4в показана, отраженная в единицах G Гомпертца на плоскость S состояний, динамика изменения алгебраического отношения средних значений модулей радиусов-векторов фазовой траектории, для которых несущей поверхностью является пространственное пересечение решетки (L-1)-ортогонального дополнения прозрачности ядер и (NCR)-ядерно-цитоплазматического отношения клеток.

Рассмотрение этих зависимостей показывает, что отношение между фазовой траекторией и состоянием, отображаемым текущими положениями ее изображающей точки, является динамическим. Оно имеет характер, соответствующий "отслеживанию" следом перемещения изображающей точки изменения состояния s на сети выхода. Это свидетельствует о том, что фазовая траектория отражает также динамический след упреждающих преобразований собственно сети изменения состояний. Такие упреждающие изменения сети могут, предшествуя активации клеток, играть роль "прокладчика" направления, своеобразного трассировщика, подготавливающего пути, обеспечивающие реализацию целевой функции. Это соответствует заданию закона отслеживания в динамике изменения состояний и управления накоплением мощности множества всех отображений состояний на множестве сетей выхода. Динамизм рассмотренного отношения является следствием динамизма перетоков и транспорта, связанных в свою очередь, с изменениями структур и мощностей множеств клеток, образующих сети входа на множестве клеток, участвующих в процессе и соответствующих накоплению множества всех отображений изменений.

Из рассмотрения приведенных зависимостей можно также предположить, что исполнению программы регулирования роста свойственен механизм плавного усреднения, на множестве сагиттальных направлений, собственных свойств обеих шаров топологического пространства как накоплений множеств, о чем говорит плавность минимумов множества усредненных проекций радиуса-вектора, проведенного из центра шара локального гомеостазиса С2. Такое исполнение программы возможно на сетях изменения состояния на перетоках, либо удержанием изображающей точки на поверхности шара локального гомеостазиса, направленным на накопление того или иного множества клеток, либо на ее отталкивание при завершенном накоплении суммарного множества всех отображений изменений состояний. Действие механизма удержания отражается в значения отношений рассматриваемых радиусов — векторов, которые каждый раз меняются на обратное в состояниях, идентифицируемых значениями ядерно-цитоплазматического отношения, достаточно близкими к моментам либо притяжения (s~0.35), либо отрыва (s~0.6), фазовой траектории от поверхности шара локального гомеостазиса.

Такой механизм мы будем квалифицировать как реализующий исполнительную, по величине и знаку отклонения, функцию на сети выхода при завершении накопления множеств всех отображений изменений состояния клеток и припишем ее, в соответствии с отображением на пересечениях, множествам клеток на сетях входа транспорта и локального гомеостазиса. Эти сети включают клетки агрессивного подмножества ортогонального дополнения, несущего фазовую траекторию. Не исключено, что эта функция как раз и является следствием и отображением упомянутой ранее перестройки первичных локальных сетей входа, изменения состояния и выхода.

Таким образом, сети входа, изменения состояния и выхода образуют последовательные и изменяющиеся во времени ситуации на структурах клеточных множеств, конкатенирующиеся в единую непрерывно изменяющуюся динамическую последовательность. Множества клеток в этой последовательности, порождаются и накапливаются первичными локальными сетями выхода на соответствующих им клеточных ситуациях сетей входа и изменения состояний. Накопление клеточных множеств на первичных локальных сетях, лишает топологическое пространство свойства дискретности. Это приводит к тому, что систему локального гомеостазиса, как биологическую систему, для которой определены динамические дискретно сосредоточенные характеристики общей теории систем, можно рассматривать как некоторый дискретно-непрерывный аналог комбинаций звеньев искусственных технологических систем управления с сосредоточенными параметрами. Заметим, что отображение сетевых конкатенаций на клеточных структурах затруднено из за непостоянства самих структур, хотя эти изменения и отражаются в топологическом пространстве.

Исполнительная функция в таком аналоге, по всей видимости, отражается плавным согласованием моментов удержания и отталкивания множеств клеток на перетоках и в транспорте. Вначале имеет место удержание взаимодействием множества клеток, покрываемых шаровой поверхностью гомеостазиса, а затем — притяжение и последующее отталкивание их в сторону фокуса, множеством клеток, покрываемых шаровой поверхностью локального гомеостазиса. Это следует из рассмотрения ситуативной динамики на граф-моделях транспортных потоков карциногенеза и его полностью определенного характеристического поля. На нем, в частности, отображены множества клеток, покрываемых сферической поверхностью локального гомеостазиса (сосредоточенные по своим параметрам в подмножества и множества на сетке характеристического поля, но распределенные в физическом пространстве биологического субстрата), объединенные с подмножествами, образовавшими в ретроспективе, первичные локальные сети изменения состояния и локальные сети входа.

Можно говорить, что исполнительная функция порождается сепаратрисными свойствами обеих шаров, реализуется по мере перемещения изображающей точки по ребру пересечения фазовых решеток к сфере шара локального гомеостазиса, порождает текущее состояния субстрата и зависима от времени наблюдения. В связи с этим, исполнительная функция в карциногенезе может рассматриваться также и как регулятор отношений агрессивности множеств клеток, покрываемых поверхностями сагиттальных пересечений решеток множеств в пространстве единичного шара.

Носитель целевой функции локального гомеостазиса и его исполнительное множество.

Отмечалось, что управление процессом трехкомпонентного роста клеточных множеств злокачественной опухоли как объектом общей теории систем, осуществляется на принципах стабилизации перемещения движущейся точки. Такой процесс обычно осуществляется как управление по скорости. Реализацию этого принципа в системе локального гомеостазиса можно проиллюстрировать, отображая траекторию изменения выходной координаты текущего состояния s биологического субстрата, отраженного в сети выхода на множестве всех его отображений и выраженного в единицах G озлокачествления Гомпертца. Отображение, относительно программной траектории, изменений управляемого состояния биологического субстрата, выраженное на мере G озлокачествления, приведено на рисунке 4г. для случая пересечения пространственных фазовых решеток (NCR)-сагиттального направления трехкомпонентного роста и его (L-1)-ортогонального дополнения Фактор закручивания траектории в пространстве отражен с помощью одиночных векторов (ортов).

При таком рассмотрении, фактор закручивания приобретает новый смысл. Он отражает уже не формальный характер управления, задающего направление перемещению изображающей точки в формальном пространстве на пересечениях фазовых решеток, а траекторию изменения управляемого, отраженного следом перемещения изображающей точки к фокусу, состояния биологического субстрата. Это состояние отражено относительно некоторого программного задания траектории, как приобретенное, при заданном качестве управления, обеспечивающего достижение множеством всех отображений изменений состояния на сети выхода за заданное (заметим, биологическое) время. Движение по этой траектории отражает путь следования управляемого объекта, находящегося в отношении со следом, трассой изображающей точки. Это вытекает из характера траектории перемещения изображающей точки, развернутой на плоскости S0G фазового пространства. Путь следования управляемого объекта и фазовая траектория, как след изображающей его состояние точки, находятся в отношении соответствия, отображаясь в разных метриках.

Отображение (L-1)-ортогонального дополнения, обладая явным минимумом в области 1.8 G притяжения шаровой поверхности локального гомеостазиса, отражает его влияние на характер траектории (NCR)-сагиттального направления. Можно предположить, что перемещение изображающей точки (L-1)-ортогонального дополнения в направлении к минимуму, отражает стремление целевой функции достигнуть пересечения с отображением (NCR)-сагиттального направления в близости к точке, определяемой абсциссой G=1.3, соответствующей максимуму отображения этого направления относительно некоторой наклонной прямой так, как это видно из рисунка. Эта прямая, соединяющая точку разворота и каноническое состояние S(G) клеточного субстрата, образует геометрическое место точек критериального оценивания качества регуляции, харктеризующего качество стабилизации роста. Регуляция относительно этого наклонного направления, производится в две полуволны различных амплитуд и периодов колебаний, находящихся в одном и том же отношении 0.8, соответствующем раковой константе (!), и полностью завершается за время канонизации процесса.

Это отражает регуляторную функцию, реализуемую клеточными множествами ортогонального дополнения, выраженную на участке регуляции качества стабилизации от точки разворота отображения (NCR)-сагиттального направления трехкомпонентного роста, вплоть до слияния обеих отображений на конечном участке, и сохраняющуюся для всех видов пересечений фазовых пространственных решеток. Заметим, что регулирование качества роста клеточного множества по величине отклонения, теоретически возможно только по его модулю.

Изображающая точка (NCR)-ядерно-цитоплазматической фазовой решетки, перемещаясь, с началом роста, параллельно оси изменения состояний 0S(G) системы координат при фиксированном значении G=1.0, и отражая изменения на множестве сетей выхода, сохраняет постоянным и равным одному гомпертцу свое положение на плоскости относительно этой оси. Этим отображается перемещение по шаровой поверхности гомеостазиса вплоть до точки, соответствующей точке отрыва и началу разворота в сторону фокуса. Такое перемещение отражает устойчивость множества всех отображений изменений внутриклеточных отношений на всех множествах входов, вплоть до наступления гомеостазического переключения.

Момент, соответствующий отрыву и развороту изображающей точки от поверхности шара гомеостазиса (0.3=1G), отображается попаданием траектории в точку разворота, что отражает гомеостазическое переключение. В этой точке, как отмечалось ранее, имеет место порождение первичных сетей изменения состояний и конкатенация сети выхода множеств клеток, покрываемых сферической поверхностью гомеостазиса, а также сети входа множеств клеток на перетоках и транспорте. Развитие сетей изменения состояний и отражается устойчивым перемещением изображающей точки к фокусу с незначительным знакопеременным изменением отклонений относительно наклонной прямой, расположенной примерно под углом в 45º по отношению к оси G системы координат и задающей качество регуляции.

Траектория изображающей точки (L-1)-ортогонального дополнения, для всех видов пересечений пространственных фазовых решеток, на всем своем протяжении, играет ролевую функцию сепаратрисы — линии притяжения в пространстве состояний, оцененных на мере Гомпертца. Эта траектория — носитель целевой функции локального гомеостазиса, а множество образующих ее клеток суть его исполнительное множество — регулятор.

Вид траектории перемещения точки, отображающей изменения состояний на мере Гомпертца, характерен для искусственных технологических систем программной стабилизации движения. В общей теории систем, систему с сосредоточенными параметрами, обладающую подобной траекторией регулирования выходной координаты, относят к классу астатических систем второго порядка, обычно управляющих перемещением объекта управления по скорости. Одна из таких систем — система стабилизации движения, на активном участке траектории, центра масс носителей искусственных спутников Земли.

Важным обстоятельством является то, что отмеченные отличительные признаки системы локального гомеостазиса, порождаются после гомеостазического переключения и после образования первичных сетей изменения состояния. Это означает, что именно этим реализуются изменения на локальных сетях входа и, в первую очередь, это связано с образованием сферической поверхности локального гомеостазиса. В этом проявляется его генеральное свойство — нарушения дискретности клеточного множества и поддержания этого нраушения, непрерывного накопления мощности покрываемых множеств озлокачествляемых клеток, накопления суммарных множеств всех отображений изменений. Но наличие хотя бы одного интегрирующего звена, как раз и является основным свойством астатической системы с сосредоточенными параметрами. Поэтому становиться ясным и справедливым, что:

- если на входе интегрирующего звена, роль которого выполняет распределенное множество накопленных подмножеств клеток, покрываемых сферической поверхностью шара локального гомеостазиса, образуется локальная сеть входа, т.е. если имеет место процесс хотя бы минимального наращивания суммарной мощности множества всех отображений на сетях изменения состояний в перетоке, независимо от характера агрессивности клеток любых состояний, координата состояния s системы локального гомеостазиса на сети выхода, будет изменяться непрерывно, начиная с образования хотя бы и одиночной клетки, обладающей признаками озлокачествления. Наличие первичного локального входа обуславливает фактор непрерывности роста, как увеличения мощности суммарного множества всех отображений изменений.

Этот вывод следует также и из того, что в силу непрерывности процесса роста, множества всех отображений входа, всех отображений изменений, равно как и всех отображений выходов, могут быть представлены направленными множествами, устремленность которых определена на мере озлокачествления в единицах Гомпертца. Это означает, что оно может быть идентифицировано в терминах систем с сосредоточенными параметрами общей теории систем, аналогично тому, как это было сделано в статье "Феномен 0.3-0.8".

Поэтому и можно говорить об отражении метаморфозы биологического субстрата изофункциональной (сходной по поведению) моделью, как моделью программно управляемой дискретной системы с квазисосредоточенными или даже с сосредоточенными параметрами.

Яков Гельфандбейн
(c) 1011494 CIPO