Группировки информационных показателей клеточного роста

Для биоматематиков

Пороговые свойства накопленной потери прозрачности клеточных ядер
Мы неоднократно отмечали свойства фазовой траектории, связанные с ее особыми точками, и в частности, с первой особой точкой, в которой отображается акт возникновения взаимодействий между подмножествами клеток гомеостазиса с множеством клеток (L-1)ортогонального дополнения для любого из сагиттальных направлений роста. Отмечалось, что взаимодействия клеточных множеств, отображенные в этой точке, имеют агрессивный характер типа "затягивания", отраженный в узел сцепления <0.3,0.13,II> проекции траектории на характеристическую сеть, отражающий скачкообразность закручивания траектории, как следствие отношения порождения.

Оптические свойства ядер клеток образуют в топологическом пространстве иерархию классификации, в которой каждый из составляющих ее объектов, обладает определенными информационными свойствами. Рассмотрим некоторые из таких свойств, имеющих пороговый характер и присущих накопленным значениям потери прозрачности клеточных ядер в окрестности первой особой точки фазовой траектории — ее отрыва от поверхности шара гомеостазиса. Этот интерес вызывается корреляцией этих свойств с положением максимума мембранной проницаемости плоскости перетока и с образованием единицы меры озлокачествления — гомпертца. Рассмотрение этих особенностей выявит отношения на множествах, способствующие генерации меры и образованию единицы измерения на ней.

Непосредственно из тройки атрибутов, отражающих положение этой точки в фазовом пространстве, видно, что каждый из них, суть множество, выраженное на присущей ему специфической мере: оптических свойств ядер клеток (идентификатор градации), частости распределения значений ядерно-цитоплазматической константы (мера вероятности), мощности множества озлокачествленных клеток (мера Гомпертца). Это означает, что положение точки, с одной стороны отражает взаимное соответствие мер, с другой — существование скрытных процессов, обуславливающих такое соответствие, а сами меры порождены на множествах. При рассмотрении особенностей точки фазовой траектории с атрибутами узла сцепления <0.3,0.13,II>, мы будем иметь в виду, что отношения между ними порождают характер фазовой траектории, как пространственной кривой.

Интенсивность клеточного роста. Активирующие свойства множества клеток баланса эквивалентности, отраженные сагиттальными направлениями роста, могут быть охарактеризованы некоторыми оценками, отражающими его "интенсивность".

Показатель интенсивности М отражает суммарное, по всем парным значениям i,j признаков состояния клеток, значение обобщенного показателя озлокачествления N<i,j> при принятой дискретности отсчета исходных данных. Такому показателю физически соответствует некоторое предельное значение роста, определенное, при устремлении интервала дискретности измерений каждого из признаков к нулю. Разница такого предельного показателя роста и его значения, соответствующего выбранной дискретности отсчетов, определяет предельную (суммарную методическую и инструментальную) погрешность исследования. Это степень нашего незнания: предельное, и соответствующее ему интегральное значение показателя интенсивности, может быть вычислено только приближенно из за отсутствия методики непрерывных измерений характеристик состояния клеток и связанных с этим погрешностей аппроксимации. Однако суждение о тенденции изменения этой погрешности, может быть произведено путем модельных вариаций дискретности оценок признаков состояния.

Для канонизированного процесса, при принятых в исследовании интервалах дискретности признаков состояний, суммарный показатель интенсивности оказался равным 665 единиц. Траектория "наискорейшего спуска", как наиболее вероятный путь роста, характеризуется величиной интенсивности, равной 〜182. Для других сагиттальных направлений роста, эта величина оказалась меньшей. Отношение М интенсивности "наискорейшего спуска" к суммарному показателю, оказалось равным 0.274, что получает свою трактовку, т.к. оно близко к значению константы перехода эпителия из состояния пластичности в состояние гиперпластичности. Отношение М суммы интенсивностей наискорейшего спуска и парциального направления <0.1-0.8,I-IV> роста, по отношению к суммарной интенсивности процесса, равно 0.43. Эта величина ранее была определена как характеристика перехода к канонизированному состоянию. Отношения интенсивностей процесса достаточно близки к отношениям констант состояния.

Понятие интенсивности М для любой выбранной системы дискретности характеристик состояния клеток, вычисленное на полном текущем множестве узлов характеристического поля, может играть роль критериальной меры для оценки завершенности процесса в задаче ракового скрининга. Его значение, вычисленное по различным цепочкам узлов решетки — путям роста, позволяет определить подмножество наиболее чувствительных и активных клеток. Упорядоченное по величине множество этих показателей, идентифицируемых принадлежностью к тому или иному текущему состоянию или направлению роста, отражает иерархию активности клеток биологического субстрата на их полном множестве.

Характеристическая функция в задаче классификации. В зависимости от принадлежности признаков i,j — аргументов обобщенного параметра той или иной фазе состояний субстрата, различные подмножества узлов сетки могут оказаться принадлежащими либо к классу эквивалентности, либо к классу толерантности. Разбиение на классы определяется характеристической функцией. В моделях, отражающих текущую динамику процесса трансформации, классы толерантности признака озлокачествления, играют особую информационную роль в выявлении и описании фазовых переходов и, что наиболее важно, — в отражении процесса структурирования системы, устойчиво управляющей ростом.

Для конкретизации понятия характеристической (разрешающей) функции, как функции двух множеств признаков П1 и П2 состояния клеточного множества, уточним, что множество градаций качественного признака, при его непрерывном изменении, рассматривается как упорядоченное множество подинтервалов интервала изменения качественных оценок признака П2. В качестве этого признака рассматривается прозрачность ядер клеток. Каждой из эквидистантных градаций прозрачности, приписывается порядковый номер в упорядоченной последовательности, что эквивалентно определению категории приоритета — предпочтения классификации.

Определим теперь характеристическую функцию F, как взвешенную (на каждом i-м значении первого признака П1) сумму взвешенных (на значениях j второго признака П2) величин обобщенного показателя N озлокачествления N<ij>, при суммировании по всем значениям j второго признака. При этом, значениям j приписываются значения абсцисс сетки характеристической плоскости, а значениям i — ее ординат. Считается, что удовлетворены все рассматриваемые условия для вероятностных распределений феномена 0.3-0.8.

Максимальное значение взвешенной на значении ядерно-цитоплазматического отношения суммы взвешенных, в свою очередь, на градациях плотности окраски ядра значений обобщенного параметра озлокачествления, оказалось равным 392. Его предельная теоретическая, для принятой дискретности отсчета величина, равна 400. Разница в 2% обусловлена погрешностями обработки исходных данных.

Рассмотрим модификации характеристической функции, удобные для практических применений.

Нормированная характеристическая функция. Для анализа динамики процессов фазовых переходов клеточных множеств, может оказаться удобным нормированное представление F0 характеристической функции. В качестве нормирующего члена удобно принять ее максимальное значение, которое обычно имеет конкретную физическую интерпретацию, связанную с характером преобразований трансформирующихся элементов множеств. Значение F0(П1) для всех значений j второго признака П2, являясь безразмерной величиной, в общем случае изменяется в пределах от 0 до 1.

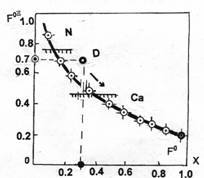
Нормированную характеристическую функцию удалось аппроксимировать уравнением параболы с фокусом в точке F0, имеющим ординату 0.228, и с достаточной точностью представить в виде соответствующего уравнения. Нормированная и суммарная характеристические кривые для процесса трансформации из спокойного состояния нормального эпителия, представлены на рисунке 1. На нем также отмечены расчетные точки и положение фокусов.

На графике выделены границы состояний и приведены характеристические числа F0NP, F0PP, F0BN, определяющие в единицах нормированной характеристической функции, границы межстратовых переходов NORMAL-PROMOTION (NP), PROMOTION-PROGRESSION (PP), PROGRESSION-BARE NUCLEUS (PB). Они оказались в окрестностях, близких "справа", к значениям соответствующих ядерно-цитоплазматических констант — инвариантов и численно отражают смену состояний субстрата. Значение фокусного расстояния параболы F0=0.228 соответствует началу перехода из состояния пластичности в состояние гиперпластичности.

Модифицированная характеристическая функция. Некоторые модификации характеристической функции, в виде двойных сумм взвешенных показателей состояния, могут оказаться важными для анализа последовательностей перетоков элементов клеточных множеств из одной фазы состояний, в другие.

Определим текущую сумму, взвешенных на упорядоченных номерах j градаций прозрачности ядер, мощностей множеств обобщенного показателя озлокачествления N<I,j>. Произведем вторичное суммирование, при котором в качестве веса используем "накопленное", и в свою очередь взвешенное на упорядоченном номере i значении плотности окраски ядра клетки, достигнутой к моменту приобретения ядерно-цитоплазматическим отношением текущего значения x. Такая двойная сумма отражает текущее накопление плотности окраски ядер.

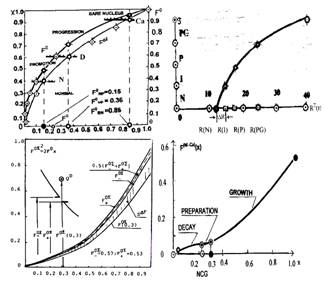
Текущее накопление плотности окраски, однако, параболой уже не отражается. Стремление аппроксимировать ее иной квадратичной зависимостью, привело к получению кривой, хотя и близкой по характеру к параболе, но с переменным фокусным расстоянием F0var — к "псевдопараболе" накопления плотности окраски ядер. Подвижность фокуса такой псевдопараболы характеризуется ее асимптотическим приближением к значению фокусного расстояния F0 параболы нормированной характеристической функции при значении ядерно-цитоплазматического отношения, характерного для голых ядер, т.е. при x=1.0 и удалением от него при уменьшении этого отношения. Характер изменение фокусного расстояния накопленной характеристической функцией, при ее аппроксимации квадратической зависимостью в виде параболы, отражается кривой, приведенной на титульном рисунке. Видно, что он близок к зеркальному отражению относительно параболы накопления плотности окраски ядра. Точки показывают вычисленные значения. Координаты <0.3,0.7> отражают существование выброса фокусного расстояния псевдопараболы. Этот выброс в точности определяет границы перехода эпителия из пластического состояния в гиперпластическое — гомеостазического переключения, и отражает скачкообразный характер его образования. Он также, отражает приоритет, в процессе гомеостазического перехода, тех внутриклеточных процессов, которые порождают увеличение плотности окраски ядра.

Функция изменения фокусного расстояния псевдопараболы снижения прозрачности ядер, соответствует переходному процессу инсталлирования конечного фокусного расстояния F0=0.228 параболы нормированной характеристической функции, как последствия гомеостазического переключения. Ее особая точка <0.3,0.7> соответствует достижению текущим фокусным расстоянием значения, соответствующего отрыву фазовой траектории от поверхности сферы шара гомеостазиса и ее закрутке, как пространственной кривой. Особенность этой точки и определяет мощность в 0.30 клеточного множества порождения, как единицы озлокачествления.

Характеристические числа. Характеристическая кривая может быть отражена цифрой, играющей роль классификационного, по характеристическому полю, порогового показателя. Ее удобно представить в виде квадратичной зависимости, связывающей интегральное значение нормированной характеристической функции, с положением инсталлированного фокуса параболы.

Интегрирование в пределах, соответствующих переходу спокойного эпителия в пластическое и далее в гиперпластическое состояние, т.е. для ядерно-цитоплазматического отношения в пределах от 0.1 до 1.0, дает значение 〜0.333, близкое к величине ядерно-цитоплазматической константы, инварианта перехода из пластического в гиперпластическое состояние. Это значение можно характеризовать как критерий критичности.

Если в аналогичном представлении, вместо нормированной, принять накопленную характеристическую функцию, то при фиксированном нижнем пределе и отслеживании во времени изменения ядерно-цитоплазматического отношения, оказывается возможным оценивать временные изменения в динамике фазовых переходов клеточных множеств по снижению окраски ядер. Такая оценка может быть произведена как разность интегральных значений обеих характеристических функций в текущих пределах, соответствующих времени наблюдения. Так, для фиксированного значением 0.1 нижнего предела, можно получить, что на полном времени роста, указанная разность стремится к 0. Это соответствует каноническому состоянию субстрата. Варьируя оба предела в таком представлении характеристической кривой, можно получать градиенты приращений значений обобщенных признаков в интересующих исследователя временных интервалах. Это характеризует скоростные свойства фазовых переходов в изучаемых процессах.

Характеристическая сетка является не только средством абстрактного отображения размножающихся множеств, но также и их функциональных свойств. Каждому элементу множества N<I,j> обобщенных параметров, на узлах сетки соответствует некоторое значение характеристической функции. Такие соответствия можно отразить формальными высказываниями и записать их на языке математической логики с помощью специальных логических операторов — кванторов.

Степень множества, как пороговый показатель роста. Множество текущих состояний клеток биологического субстрата образуется множеством истинных подмножеств клеток текущих состояний. Это является следствием динамизма функциональных взаимодействий, порождающих клеточный транспорт.

Количество клеточных подмножеств также динамично и находится в отношении соответствия с текущим изменением структуры универсального множества. Изменение количества подмножеств образуется как функция R(A) накопления множества А собственных подмножеств текущего состояния. Эта функция отображает пороги роста количества подмножеств, образующих универсальное множество. Количество таких подмножеств, независимо от характера отношений между ними, иногда называют степенью множества. Рассмотрим динамику степени множества выборки A клеток, из их генеральной совокупности A, как упорядоченную последовательность порогов роста, отражающих страты состояния.

Множество клеток А канонического состояния, формируется накопленным множеством подмножеств клеток текущих состояний, изменяющихся в зависимости от входящих в него собственных подмножеств, включая пустое множество (их множество отображено на сетке характеристического поля). Степень множества для канонического состояния субстрата максимальна. При принятой дискретности отсчета признаков состояния x, L, и классификации состояний субстрата на страты N, I, P, PGO, PG, она оказалась замороженной на величине R(A)=40 для канонического состояния, для гиперпластического состояния на величине 25, для пластического состояния — 18, а для нормального состояния, с учетом включенного в него множества из 4-х подмножеств клеток пластического состояния спокойного эпителия — 15. Напомним, что переходное состояние PG0 отражается узлом сцепления <0.3,II> на множестве клеток баланса эквивалентности, образованного объединением трех (под)подмножеств клеток состояния N, I, P. Если эти три подмножества исключить из множества подмножеств клеток нормального состояния, то можно говорить, что степень множества канонического состояния R(A) образуется множеством клеток степени 12, а исключенные подмножества баланса эквивалентности, "скачком" формируют стартовое, инициальное множество PG0 отправления из нормального состояния в состояние PG. Этот скачок отражается на многих характеристиках процесса и является, по существу, его запуском. Это еще раз подтверждает особое значение точки отрыва фазовой траектории от сферы гомеостазиса и ее значимость как единицы меры озлокачествления.

В динамике процесса трансформации зависимость текущего состояния биологического субстрата от степени множества отражается кривой, близкой к параболе. Ее аргументом является накопление степени множества, а функцией — упорядоченная эквидистантная последовательность состояний, идентифицируемых аналогично тому, как это было сделано для градаций прозрачности ядра клетки — эквидистантными идентификаторами следования. Эта кривая приведена на рисунке 2. Приращение R на этом рисунке. отражает положение подмножества клеток узла сцепления <0.3,II> состояния PG0. Сходство ее с параболой характеристической кривой, подтверждает уверенность, что последовательность пяти градаций L прозрачности ядер клеток 0-I-II-III-IV эквидистанта последовательности пяти текущих страт состояний N-I-P-PG0-PG клеточного множества и отражает текущее состояние субстрата.

Степень множества в динамике размножения клеточной популяции является переменной величиной, отражающей работу механизма транспорта, а следовательно, и рост опухоли. В зависимости от степени конкретизации структуры клеточных ситуаций, принятой системы классификации состояний и динамизма кинетики, степень множества может отражаться наборами иных численных значений своих параметров. В частности, она может быть конкретизирована до уровня структуры множества подмножеств клеток, образующих узел характеристической сетки.

Степень множества является пороговым, для каждой страты состояний, показателем роста. Порядку следования 15,18,25,40 степеней множеств последовательности состояний субстрата, соответствует отношение 0.62:0.72:0,83 группировок клеток по подмножествам (или порожденное этими группировками накопление атипии 1.61:1.38:1.21 на годографе процесса , приведенном в статье "Феномен 0.3-0.8"). Эти соотношения отражают динамизм перегруппировок множества клеток гиперпластического состояния в генеральное множество подмножеств степени клеток канонического состояния и находятся в отношении соответствия с множеством констант состояния. Соотношению группировок, в свою очередь, соответствует соотношение, отражающее баланс раковых констант 0.86:0.86, приводящий к отражению отношения 1.0 завершенности процесса. Множество этих соотношений упорядочивается в ранее упоминавшийся треугольник клеточного транспорта, который образует набор критериев переходов алгоритма целевой функции карциногенеза.

Переключающее множество гомеостазического перехода. Можно показать, что переключающее множество клеток Q отображается площадью, заключенной между двум параболами. Одна из них — аппроксимирующая парабола суммарной (накопленной) характеристической функции, с фокусным расстоянием F0=0.7, другая — некоторая "переключающая" парабола с фокусным расстоянием 0.5. Фокус второй параболы отражает интервал разрыва непрерывности отношения совершенного строгого порядка на первой параболе, внутри которого происходит скачкообразное появление переключающего клеточного множества Q. Разность фокусных расстояний этих парабол, определяет приращение мощности переключающего множества Q=0.15 и отражает разрыв непрерывности значений х аргумента ядерно-цитоплазматического отношения такого, что в середине разрыва фокусное расстояние переключающей параболы равно 0.5. Образование скачка QD фокусного расстояния накопительной параболы в пространстве формирования накопительного переключающего множества Q показано на рисунке 3.

Величина разрыва непрерывности отношения совершенного строгого порядка на суммарной характеристической функции, определилась приближениями 0.57 снизу и 0.53 сверху таким образом, что этот разрыв, нарушив отношения на элементах биологического субстрата, оказался равным 0.04 и лежащим в интервале значений ядерно-цитоплазматического индекса между 0.28 и 0.32. Это отражает длительность во времени акта переключения системы клеточных отношений, как промежутка времени образования значений x ядерно-цитоплазматического отношения в интервале от 0.28 до 0.32, не более чем у 4¸5 % клеток.

Накопление мощностей функциональных клеточных множеств. Такое накопление отражается относительным изменением площадей функциональных областей физической реализации разрушения отношений гомеостазиса DECAY, трассировки направлений роста PREPARATION и собственно роста GROWTH, по мере развития процесса трансформации.

Накопление мощностей клеточных множеств Fd в области decay, характеризует уменьшение сопротивляемости клеток состояния гомеостазиса на интервале значений от 0.05 до 0.22 роста х ядерно-цитоплазматического отношения и обуславливает подготовительный процесс перехода от абстрактной возможности возникновения процесса озлокачествления, к его физической реализации. Такое накопление, как суммарная разность роста в соответствующих пределах, оказалось равным 0.0545.

Накопление мощностей клеточных множеств FP в области PREPARATION, характеризует процесс подготовки, клетками множества баланса эквивалентности, акта переключения и перехода клеточного субстрата к процессу неравновесного роста GROWTH. Такое накопление оказалось равным 0.0322.

Накопление мощностей клеточных множеств FCa в области GROWTH характеризует процесс неравновесного роста, завершающийся трансформацией биологического субстрата в каноническое состояние. Такое накопление оказалось равным 0.3905. При этом, накопление мощности клеточных множеств на замкнутом интервале значений роста ядерно-цитоплазматического индекса от 0.05 до 1.0, оказалось равным 0.4772.

Накопление мощностей клеточных множеств FCa в области GROWTH, с точностью до точности обработки данных исходного описания, совпадает с мощностью множества подмножеств активирующих клеток состояния (страты) PROMOTION баланса эквивалентности. Так как оба значения мощностей получены в относительных величинах и равны, такое совпадение отражает полное переключение клеток этого подмножества в подмножество клеток баланса толерантности.

Накопление мощности множества подмножеств озлокачествляющихся клеток, показано на рисунке 4. Эти накопления находятся в отношении соответствия с областями их физической реализации. Зависимость роста множества теряющих сопротивляемость клеток состояния гомеостазиса на участке DECAY, соответствует решению дифференциального уравнения роста популяции на этом участке, известного как Гомпертцовская кривая.

Накопление роста отражает пороговое условие гомеостазического переключения, которое требует наличия "15% клеток состояния initiation и образования разрыва отношения совершенного строгого упорядочения непрерывности накопленной характеристической функции на интервале от 0.28 до 0.32, при наличии в этом интервале, не более 4¸5 % клеток.

Еще раз отметим, что множество клеток, отображаемых в накопление FCa, отражает результат перемены системы отношений совершенного строгого упорядочения на отношения строгого упорядочения, следствием чего является переход из равновесного состояния субстрата в неравновесное, и дальнейший рост опухоли. При этом, как уже говорилось, каждое отдельное образовавшееся подмножество клеток, остается на области своего отправления дважды упорядоченным отношениями совершенного строгого и строгого порядков, т.е. максимальным совершенным подмножеством, а подмножество переключения Q, находясь в отношении порядка, делается изолированным в точке <0.3>. Это еще раз подтверждает, что возникновение злокачественного роста — гомеостазический переход, есть следствие изменения отношений порядка, в свою очередь дочерних относительно отношений порождения.

Иерархия классификации в топологическом пространстве свойственна высоко организованным системам. Она образуется системой характеристических объектов — пространств, поверхностей, плоскостей, пространственных кривых и линий на плоскости, характеристических функций и чисел различной природы — инвариантов, констант, показателей состояний и особых точек. В ней отражаются свойства решетки клеточных множеств, узлов сцепления на решетке, направлений активации и роста. Она представима графом и деревом классификации, элементы и составные части которых находятся в отношениях, большинство которых имеет смысл порогов, как величин, достигающих определенного значения. Это отражает системные свойства процесса опухолевого роста, как объекта общей теории систем.

Классификация и группировка информационных показателей по их происхождению, устанавливает специфическую информационную систему, удобную для реализации на ней механизма распознавания, аналога математической модели феномена восприятия.

К вопросу о персептроне. Рассмотрим соображение, высказанное на форуме сайта Лоренсом, о разработке персептрона, решающего задачу зрительного восприятия морфологической картины клеточного поля и проведем некоторые параллели между персептроном и рассматриваемой моделью. Это удобно сделать именно при рассмотрении особенностей обрабатываемой информации.

Персептрон обычно рассматривают в качестве устройства, реализующего задачу зрительного анализатора оптических изображений. Алгоритм распознавания в персептроне, осуществляет разделение классов элементов сложного образа, воспроизведением трех слоев нейрона — нервной клетки с несколькими (возбуждающими или тормозными) входами и одним выходом (модель Мак-Каллока — Питса). Нейрон возбуждается и посылает импульс в том случае, если число сигналов на возбуждающих входах превосходит число сигналов на тормозных входах на некоторую величину, называемую порогом срабатывания нейрона. В 1957г. американский учёный Ф. Розенблатт построил персептрон в качестве простейшей модели мозга.

В персептроне реализуется обучаемая распознающая система с корректируемой в процессе обучения, линейной решающей функцией на множестве вторичных признаков, являющихся фиксированными случайно выбранными линейными пороговыми функциями от первичных признаков. Пороговый элемент решает задачу пороговой логики структурной теории автоматов. На вход персептрона поступает сигнал, представляющий собой набор первичных признаков, по которым вычисляются вторичные признаки. Каждому такому признаку соответствует линейная функция и порог, признак принимает значение 1, если соответствующая линейная функция превышает порог, в противном случае она равна 0. Для каждого из классов вычисляется разделяющая (характеристическая) функция, как линейная относительно вторичного признака. При вычислении характеристической функции вторичным признакам придаются веса и решение принимается в пользу того класса, которому соответствует характеристическая функция, получающая для данного входного сигнала наибольшее значение. Обучение заключатся в коррекции весов при каждой ошибке распознавания, т.е. при каждом случае несовпадения решения, выдаваемого персептроном и истинного класса. Персептрон способен решить задачу обучения, если распознаваемые классы сигналов отображаются в пространстве вторичных признаков в выпуклое множество.

Погрешности распознавания персептрона достаточно велики. Поэтому производились многочисленные попытки расширить его возможности путем усложнения структуры, в которой сигналы от чувствительных элементов передаются через несколько слоев многовходовых пороговых элементов и лишь затем поступают на входы решающих элементов. Этот путь приводит к потере простоты и ясности обучения. Однако схема персептрона, несмотря на малое практическое применение, сыграла большую роль в проблеме моделирования разумного поведения, обучения и самообучения различных кибернетических устройств.

Алгоритм построения математической модели карциногенеза в топологическом пространстве, структурно и функционально схож с алгоритмом построения персептрона, что видимо, и породило предложение рассмотреть этот вопрос. Их сравнение показывает, что он реализует ту же сущность восприятия, но иным путем. Но это лишь внешнее сходство. Используя множество первичных признаков состояния (ядерно-цитоплазматическое отношение и прозрачность ядер) клеточного множества, он также преобразует их во множество вторичных, обобщенных признаков — показателей состояния, характеризующихся числом, и взвешивает их на отношениях порождения. Применение решающего правила (классификации), на некотором множестве значений характеристических функций и фазовой траектории, воспринимаемых как пороговые, приводит к решению задачи распознавания морфологической картины, как задачи зрительного анализатора оптических изображений — их зрительного восприятия. Важнейшей особенностью модели, дающей ей ряд предпочтений в решении конкретной задачи, является реализуемая ею заместительная и познавательная функции, которыми персептрон не обладает.

Несмотря на принципиальные различия в понимании самого подхода к понятию "зрительное восприятие", применительно к этим, далеко не равнозначным по генезису и назначению системам, и следующие из этого принципиальные различия методических, структурных, алгоритмических и системных подходов, использование идентичного по характеру информационного описания объекта восприятия, приводит к достижению единой цели. Рассмотрение методов построения модели, функциональных особенностей структуры и отношений элементов, дают все основания утверждать, что распознающая способность модели образует систему восприятия "направленного действия", аналогично тому, как сама она изофункциональна по поведению клеточному множеству метаморфозы биологического субстрата.

В отличие от персептрона, имеющего широкое назначение и предназначенного для воспроизведения, хотя бы и не адекватно, но функции мозга (в том числе и для восприятия морфологической картины клеточного поля), построение и применение анализатора в виде множественной модели роста, ограничено сугубо утилитарной, специфически направленной конкретной задачей рассмотрения видимого злокачественного роста клеточных множеств.

Такая целевая направленность и настройка модели на решение конкретной задачи на специфически упорядоченной системе описания исходного состояния, устранила необходимость многовходовости и обучения, свойственные персептрону, существенно упростила процесс распознавания, сделала его более надежным и придала модели мощную заместительную и познавательную функции. Модель карциногенеза — функциональный, специфически направленный аналог модели восприятия, инструмент распознавания и прогноза.

Если же говорить о создании персептрона, предназначенного для решения задач в области злокачественного роста, то его разработке, как некоторого "квазиперсептрона", специфического решателя, способствует существование специализированных устройств сбора данных исходного описания в формате, применяемом для получения решетки клеточных множеств, которые исключают разработку специальной сетчатки персептрона из светочувствительных элементов. Одно из таких устройств, реализующее измерение ядерно-цитоплазматического отношения и выделение констант состояния (Tanaka N, Ikeda H, Ueno T, Mukava A, Watanabe S, Okamoto K, Hosoi S, Tsunekawa Sh. Automated cytology screening system (CYBEST model 4): integrated image cytometry system // Applied optics. — 1987. — Vol.26. — №16. — P.3301-3307), заимствовало наши идеи по патенту USA 3976827 (Альен И.К., Авдеев И.И., Гельфандбейн Я.А., Ершов Б.Н., Никоненко A.В., Попов Ю.А., Хесин А.Я., Янсон Б.А. Apparatus for evaluаting characteristics of the images of objects). Устройство по этому патенту еще в 70-х годах было создано в АН ЛССР (гос. премия СССР в 71г., ЛССР в 70г.). Однако применение специализированных устройств считывания исходной информации, лишает персептрон одной из его основных функций — видения на специальной сетчатке, сохраняя, тем не менее, функцию "нейронного" решателя.

Отметим, что существует также хорошо разработанная система обучения, работающая на пороговых принципах, схожих с используемыми в персептроне (Осис Я. Я., Гельфандбейн Я. А., Маркович З. П., Hовожилова Н. В. Диагностирование на граф-моделях. М., Транспорт, 1991) и, кроме того, решающая прогностические задачи "System of forecasting of outcomes of surgical operations" (Dalhousie University, Halifax, 1955), разработанная автором на базе принципов, содержащихся в выше указанной монографии. Использование идей, реализованных в этих системах, не приведет к существенному искажению принципов решателя, заложенных в персептрон Ф.Розенблаттом.

Проблема высококачественного многослойного персептрона, как проблема всецелевого средства зрительного восприятия существует независимо от моделей распознавания любого назначения..

Так или иначе, персептрон, реализуя одну из функций мозга, предназначен для решения, с тем или иным качеством, лишь узкой задачи распознавания, но не "осмысливания" полученного результата.

Яков Гельфандбейн
(c) 1011494 CIPO