Пересечения пространственных фазовых решеток карциногенеза
Для биоматематиков
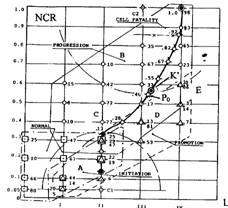 Шары гомеостазиса и мера озлокачествления на них
Шары гомеостазиса и мера озлокачествления на них
Наблюдаемый под микроскопом биологический субстрат, представляет собой одномоментно изъятый (элиминированный) клеточный материал, случайный по месту (топографии), времени возникновения и развития процесса озлокачествления, а также и по времени его изъятия. Это статический, случайный и уникальный срез динамических изменений — роста опухоли и даже серии последовательных срезов, не могут отразить все многообразие динамики клеточного поля. Методика получения материала не позволяет наблюдать и численно оценивать непосредственно, ни предысторию, ни будущее развитие клеточных множеств, хотя и доставляет некоторую возможность их "замороженной" оценки, например — на вероятностной мере.
С позиций моделирования карциногенеза методами множественной идентификации, по описанию и оценке элиминированного материала, должны быть отражены не просто достигнутые изменения состояния, но и динамизмы этих изменений, причем на всем интервале времени, начиная с момента (не наблюдаемого) начала процесса инициации. Такая модель должна отражать динамизмы процесса и управления им на всем клеточном множестве, его отдельных подмножествах, их пересечениях и объединениях (решетке множеств), в том числе — по каждой отдельно взятой клетке, включая изъятые для исследования.
Пространственные фазовые решети. Отражая направление роста, фазовые сагиттальные оболочки, в силу своей мажоритарности, покрывают полное размножающееся множество подмножеств клеток характеристического поля, включая и их пустые подмножества. Этим увеличиваются покрываемые объемы и игнорируется аксиоматика классов состояний. В свою очередь, это затрудняет и искажает (особенно в области инициальных состояний), оценку динамики озлокачествления с учетом транспортных путей из пространства отправления, в соответствующие тому или иному сагиттальном представлению пространство прибытия, как в подпространства s состояний S решетки множеств озлокачествляющихся клеток.
По построению области отправления трансформирующихся клеток отображаются на множестве клеточных подмножеств системой их открытых подмножеств так, что пустое множество и все пространство, их объединение и пересечения также являются открытыми множествами. Это придает множеству исходного описания на характеристическом поле природу топологического пространства. В этом пространстве может быть отображен характер функциональных взаимодействий между множествами подмножеств клеток, конкретизирующий их взаимодействия на различных сагиттальных направлениях роста. Геометрически такое отображение образуется на гранях пересечений разделительных поверхностей в границах подпространств, покрываемых пересекаемыми фазовыми пространственными решетками. Пересечения решеток образуют поверхности, разделяющие сагиттальные подпространства. Сагиттальные подпространства отражают специфические свойства породивших эти пространства клеточных множеств, приобретенных ими (клетками) в динамике кинетических процессов транспорта и перегруппировок по множествам функциональных подмножеств.
Отличие фазового пространства от топологического определяется, в данном случае, заданием области отправления. Если в первом пространстве эта область задается нормированным ростом на древесном порядке, то во втором — множеством подмножеств значений параметров состояния отдельных клеток на решетках пересекающихся сагиттальных представлений. При этом, множества трансформирующихся клеток, покидая пространства своего отправления образуют топологию, на множестве архитектурных элементов которой, в каждый текущий момент времени, каждая из транспортируемых клеток, определяется топографически как в пространстве прибытия. На топологии, как на отображении транспорта конкретных клеточных множеств, устанавливается мера озлокачествления. В отличие от качественной, сопоставительной меры на идентификаторах древесного роста или вероятностной меры на распределениях ядерно-цитоплазматического отношения, в пространстве топологии она принимает естественный характер неотрицательной счетно-аддитивной функции клеточного множества. Это позволяет производить на клеточных множествах анализ, при котором все рассматриваемые объекты аппроксимируются числами или их комплексами.
При введении меры возникают чисто математические проблемы. В частности, для конкретизации отображения сагиттального пространства на мере, и его сужения до области прибытия, покрываемой сагиттальной оболочкой, но ограниченной внутри ее границами, соответствующими установленным аксиоматикой классов состояний, из-за собственных особенностей оболочек, оказывается необходимым использовать отображения пространственных решеток, имеющих характер ортогонального дополнения. Такое дополнение образуется как множество всех элементов векторного пространства, в котором определено скалярное произведение. В частности, оно было получено для L-сагиттальной решетки, отражающей парциальное направление роста, порождаемое изменением прозрачности ядер, как множества всех элементов фазового подпространства, ортогональных каждому элементу фазового NCR-сагиттального подпространства, покрывающего направление роста, отраженного изменениями ядерно-цитоплазматического отношения.
Пересечения пространственных фазовых решеток. Пространственные фазовые решетки образуются как пересечения фазовых решеток, в виде кусочно-непрерывных поверхностей, "вырезаемых" в фазовых сагиттальных подпространствах, путем вычленения (под)подпространства, "натянутого" на столбчатые наборы решетки множеств характеристической плоскости, в соответствии с аксиоматическим представлением состояний клеточного субстрата.
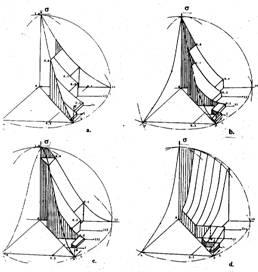 Такие кусочно-непрерывные поверхности — пространственные фазовые решетки для основных сагиттальных представлений — инициального (а), прозрачности ядер (b), ядерно-цитоплазматического (с) и ортогонального относительно прозрачности ядер (L-1)сагиттального направления роста (с), показаны на рисунке 1.
Такие кусочно-непрерывные поверхности — пространственные фазовые решетки для основных сагиттальных представлений — инициального (а), прозрачности ядер (b), ядерно-цитоплазматического (с) и ортогонального относительно прозрачности ядер (L-1)сагиттального направления роста (с), показаны на рисунке 1.
Они, как и ранее, определены в пространствах, ограниченных своими сагиттальными линейчатыми оболочками, рост также рассматривается как трехкомпонентный, а текущие состояния субстрата s — как его отображения. Однако, в этом случае отображение области отправления клеточных множеств в область прибытия, конкретизируется конфигурацией решетки множеств отправления сагиттального представления в соответствии с аксиоматикой клеточных множеств, имеющей ступенчатый характер, отражающий специфику графов сагиттальных направлений роста.
Ступенчатость отражает пределы непрерывности, определенные разбиением классификации клеточных множеств на подмножества на характеристическом поле. Именно на пересечениях таких решеток, отображается множественная модель озлокачествления, удовлетворяющая всем предъявляемым к ней требованиям.
Пересечения решеток связываются с предположением суперпозиции роста по всем его сагиттальным направлениям. Однако пересечения непосредственно сагиттальных фазовых оболочек, в силу их инъективного соответствия — упорядочения вложением, как отмечалось выше, получено быть не может, хотя могут быть найдены пересечения решеток этих оболочек, с сагиттальными пространственными решетками ортогонального дополнения. В качестве такого дополнения мы будем рассматривать (L-1)сагиттальную решетку (d), соответствующую решетке L-cагиттального представления. C формальной точки зрения это означает использование тех же (образующих L-сагиттальную решетку) множеств клеток, но отображенных в другое метрическое пространство, сохраняющее расстояние между любыми двумя точками таким образом, что отображение разностей роста соответствует отображению разности изменений состояния. Имеет место отображение одного метрического пространства в другие метрические пространства, называемые изометрическим отображением. Свойство пересекаемости решеток с их ортогональным дополнением обусловлено ортогональностью двойки множеств <i,j> аргументов исходного описания <x,L> на характеристической плоскости, где они образовали ортогональную систему.
Фигуры на рис.1 отражают пределы и предельные поверхности тех подпространств, которые вырезаются из областей прибытия множеств трансформирующихся клеток по сагиттальным направлениям роста, определяемым их аксиоматическими представлениями.
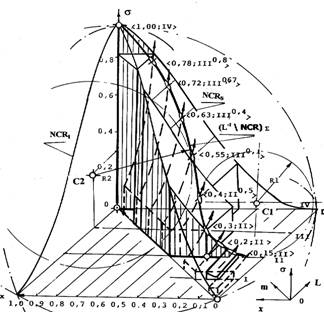 На другом рисунке показано пересечение двух пространственных фазовых решеток — (L-1)ортогонального дополнения (d) решетки сагиттального направления прозрачности ядер и NCR-сагиттального направления (c) их ядерно-цитоплазматического отношения. Пересечения пространственных фазовых решеток образуют горизонтально-линейчатые разделяющие поверхности.
На другом рисунке показано пересечение двух пространственных фазовых решеток — (L-1)ортогонального дополнения (d) решетки сагиттального направления прозрачности ядер и NCR-сагиттального направления (c) их ядерно-цитоплазматического отношения. Пересечения пространственных фазовых решеток образуют горизонтально-линейчатые разделяющие поверхности.
Фазовая траектория изображающей точки рассматривается как зависимость роста от парного соответствия ядерно-цитоплазматического отношения x и прозрачности ядер L, а ее текущее положение на архитектуре топологии — как отражение текущего состояния s и времени t. Их отображения проецируются в узлы пересечений пространственных фазовых решеток на плоскостях системы координат образованного топологического пространства. Цифрами в ломаных скобках показаны значения координат проекций узлов пересечений на основание системы координат — характеристическое поле.
Границы пересечения горизонтальных линейчатых поверхностей образуют линию перетока сложной конфигурации, как грань вертикальной линейчатой поверхности, находящейся под оболочкой и делящей покрываемое ею пространство на два подпространства. Она, для каждой из пар образующих ее сагиттальных представлений, отражает характер транспорта клеточных множеств, находящихся в отношении двух типов функциональных взаимодействий.
На начальных участках равновесного состояния <0.05,II>, <0.15,II>, <0.2,II>, <0.3,II>, внутриклеточные отношения взаимодействий на множествах клеток в системе гомеостазиса, отображаются траекториями, прилегающими к поверхности сагиттальных оболочек вдоль секущей плоскости II градации прозрачности ядер клеток. Геометрически это представляется тем, что клеточное множество системы гомеостазиса покрывается малой сферой. Эта сфера, в свою очередь, вписана в сферу единичного шара и касается ее изнутри. Ее радиус соответствует мощности накопленного переключающего множества клеток Q: в области значений <i,j>=<0.05÷0.3,II> аргументов обобщенного параметра озлокачествления, след пересечения горизонтальных линейчатых поверхностей, имеет границы, лежащие на этой сфере. Диаметральное сечение шара формируется пересечением оболочек в этих областях отправления клеток.
Это означает, что областей отправления, в смысле транспорта озлокачествляемых клеток, в шаре ограниченном этой сферой, фактически не существует и, находясь в состоянии покоя, клеточные множества, покрываемые ею, в транспортный процесс не вовлекаются. Круговая форма границы пересечения решеток множеств клеток нормального состояния, отражает постоянство внутриклеточных отношений на этих множествах и обусловленное этими отношениями равновесное состояние (покоя) биологического субстрата.
Шар гомеостазиса. Малая сфера образует покрытие клеток равновесного состояния. Она формирует шар гомеостазиса, касающийся своим диаметральным сечением линейчатой поверхности пересечения решеток в плоскости L=II, прозрачности ядер.
Это шар — внешней, относительно фазовой траектории кривизны, с центром в точке C1.
Удерживая след траектории изображающей точки на шаровой сфере в окрестностях участка касания i£0.3,II, он играет роль сепаратрисной поверхности.
Начиная с точки <0.3,II>, соответствующей топографии множества подмножеств агрессивных клеток баланса эквивалентности, траектория отталкивается от шара и, находясь на оболочке, разворачивается в сторону фокуса фазового пространства. Вращаясь, и отражая сложное движение изображающей точки, она изменяет свое направление в сторону увеличения значений градаций прозрачности ядер. Такое поведение траектории может отражать высокую восприимчивость, реактивность клеточных множеств, реализующих включение новых механизмов целевого управления, порожденных гомеостазическим переключением, воздействующих на молекулярные процессы, отражающиеся в прозрачность ядра.
Можно предположить также, что с позиций механизмов управления процессом, отталкивание траектории изображающей точки, наблюдаемое на всем множестве пересечений пар сагиттальных направлений, является следствием групповых межклеточных взаимодействий между активирующим множеством подмножеств клеток баланса эквивалентности, характеризующимся граничным положением <0.3,II> на решетке исходного описания, и аналогичным по мощности множеством клеток активирующей решетки (L-1)ортогонального дополнения, пересекающимися в этом узле характеристического поля.
Важным обстоятельством является то, что рост дерева, соответствующий точке отталкивания, на решетке ортогонального дополнения, как и на ее прообразе, численно равен накопленной мощности множества Q переключения, равной 0.13, но выражен в нормированных единицах накопленной потери прозрачности ядер клеток. В дальнейшем, по мере увеличения парных значений <i,j> аргумента обобщенного показателя озлокачествления, интенсивность взаимодействия множеств клеток на решетках возрастает, образуя траектории, обладающие для каждого из пересечений специфическими особенностями. Их усредненное, по парам множеств сагиттальных направлений роста значение, образует фазовую траекторию процесса в топологическом пространстве. Построение такой характеристики процесса означает, что он может быть представлен, описан и оценен теми же методами общей теории систем, что и процессы искусственных технологий и, поэтому, его можно отнести к классу естественно-технологических процессов (А.М.Уголев Естественные технологии биологических систем. М. Наука, 1987).
Внешний шар, определяющий начальную внешнюю кривизну линейчатой поверхности пересечения пространственных решеток множеств для такой траектории, отражает систему внутриклеточных взаимодействий начального, относительно роста, состояния гомеостазиса и не зависит от вида и характера пересекающихся в карциногенезе решеток. Его центр С1 лежит в точке с координатами <0.05,0.3,II> в фазовом пространстве внутри единичного шара, располагаясь, таким образом, в плоскости INITIATION - II градации прозрачности L ядер с превышением в 0.3 над основанием системы координат. Значение этого превышения, равное 0.3, соответствует значению дисплазионной константы на вероятностной мере, определяющей начало перехода клеток из состояния покоя в пластическое и далее в гиперпластическое состояние, что отражает переход от внутриклеточных отношений в системе гомеостазиса к системе групповых межклеточных взаимодействий в системе локального гомеостазиса.
Полностью определенное характеристическое поле. Проекция шара внешней кривизны на характеристическую плоскость, дополняет её, покрывая ту часть A ее области, которая отражает множества клеток, находящихся в состоянии INITIATION (титульный рисунок) и содержит множество клеток узла сцепления <0.3; II> и его ближайших окрестностей, образующих баланс эквивалентности. Полностью определенное характеристическое поле содержит точки парных соответствий рассмотренных пересечений для состояний NORMAL; PROMOTION и PROGRESSION.
Узлы проекции фазовой траектории на характеристическую сеть, определенную на таком поле, оцифрованы мощностью клеточных множеств пересечения, отображенной в относительные значения роста. Дуги, образованные проекциями диаметральных плоскостей, указывают границы шара гомеостазиса, а также оболочки шарового сегмента шара локального гомеостазиса с центром С2.
Клеточное множество узла сцепления<0.3;II> ответственно за накопление переключающего множества Q, образуя его, и реализуя переключение системы гомеостазиса в систему антигомеостазиса. Проекция шара гомеостазиса, однако, не покрывает подмножеств клеток с отношением равным 0.3 и менее, но обладающих, одновременно, нулевой градацией прозрачности ядер. Это уточняет структуру и состав переключающего множества Q с учетом аксиоматического представления решетки клеточных множеств, а также отношение "градация прозрачности ядра — состояние". Подготовка переключения и его осуществление реализуются в ближайших окрестностях сферы гомеостазиса.
Полностью определенное характеристическое поле также конкретизирует ту роль целевой функции локального гомеостазиса, реализация которой отражается в значение градации прозрачности ядра. Множество подмножеств клеток, обладающих прозрачностью ядра в пределах 0-I градации, принадлежит к состоянию NORMAL, в пределах I-II - к состоянию INITIATION, в пределах II-III - к состоянию PROMOTION, а в пределах III-IV - к состоянию PROGRESSION. Можно полагать, что критическим состоянием субстрата является состояние PROMOTION.
Отсюда следует важный вывод: номера I,II,III,IV градации L прозрачности ядер, идентифицирует четыре основные страты состояний субстрата. Это означает, что парное соответствие аргументов x и L обобщенного показателя N(x,L)=N<I,j> озлокачествления, отражает соответствие значения ядерно-цитоплазматического отношения клеточного множества страте состояния, а мощность N клеточного множества, на котором это соответствие проявляется, его уровню (множеству фаз состояния) на страте. Вычленение парных соответствий аргументов, равносильно вычленению клеточных множеств страт состояний. Это объясняет робастность выбранных градаций прозрачности ядер — независимость качества оценки состояния от незначительных отклонений в оценке оптических характеристик ядер клеток: "попадание" в страту проще "попадания" на ее уровень.
Мера озлокачествления. Пусковой, инициальный рост, соответствующий внешнему радиусу кривизны поверхности пересечения каждой пары решеток из их множества, независимый от его последующих сагиттальных направлений роста, определяющий положение центра C1 шара гомеостазиса и отражающий мощность направленного множества Q переключения, определим как меру.
Эта мера устанавливает границу, за которой, изменение накопленных значений аргументов <i,j> обобщенного параметра озлокачествления, влечет за собой гомеостазическое переключение системы внутриклеточных отношений в систему межклеточных взаимодействий или, что то же — системы гомеостазиса в систему локального гомеостазиса. Внешний круговой радиус кривизны поверхности пересечения решеток множеств клеток, есть инвариант всего множества динамических отношений в карциногенезе.
Значение роста равное 0.3, будем называть единицей Гомпертца и обозначать как G, в честь английского математика Benjamin'a Gompertz'a (1779-1865), впервые получившего и решившего уравнение роста размножающихся популяций. Единица роста позволяет сопоставлять и оценивать на естественной мере древесный рост, изменяемость текущих состояний, а также различных параметров и элементов фазового и топологического пространств. Максимальный рост опухоли и финитное состояние биологического субстрата оцениваются в 3, (33)G.
Шар радиуса 1G, определенный в пространстве топологии как шар внешней кривизны траектории роста, будем называть шаром гомеостазиса независимо от характера пар сагиттального представления, образующих соприкасаемую с ним оболочку и видов фазовых решеток, образуемых пересекающимися множествами.
Шар локального гомеостазиса. Траекториям изображающих точек пересечений всех видов фазовых решеток, могут быть поставлены в соответствие шары внутренней кривизны. Они определяются различными точками касания с фазовой траекторией для различных сагиттальных представлений внутри сагиттальных оболочек, но имеют единый для всех пересечений центр С2, расположенный на плоскости отсчета прозрачности ядер в точке <1.0, 0.3, III> в сечении ее III градации PROMOTION, при значении роста, равном, как и для шара гомеостазиса, одному гомпертцу — 1G. Радиусы внутренних шаров кривизны зависят от положения точки касания с фазовой траекторией, лежащей на грани линейчатой поверхности, образуемой пересечениями решеток. В частности, для сагиттального пересечения (d) (L-1)ортогонального дополнения решетки сагиттального направления прозрачности ядер и NCR-сагиттального направления, он оказался равными 1.5G. Для пересечения этого же ортогонального направления с направлением роста инициального сагиттального направления (а), он равен 1.66G.
Таким образом, основание системы координат L0X, образуя основание шарового сегмента, расположенного в пространстве единичного шара, ограниченном пересечением сагиттальных оболочек, играет роль трансверсальной плоскости, отсекающей, для рассматриваемых сагиттальных пересечений, шаровые сегменты высотой h=-0.56 и h=-0.66 соответственно. Оболочка каждого из сегментов, покрывает в выбранной системе координат фазового пространства, множество подмножеств клеток на решетке характеристического поля, находящихся в системе отношений локального гомеостазиса — область B (титульный рисунок).
Множество дискретных сагиттальных представлений роста на характеристическом поле, интегрировалось в непрерывную функциональную зависимость между двумя переменными, при которой каждому значению одного переменного x соответствует определенное значение другого переменного L (и обратно). Сагитальность направления роста, при этом, отразилась в его динамику предельным отношением — направлением касательного вектора, обобщающего понятие производной по направлению, т.е. в скорость роста. Пространственные фазовые решетки карциногенеза содержат информацию о скоростных характеристиках процесса, и отражают ее характером фазовой траектории.
Все элементы структуры полученной модели имеют четкую интерпретацию на мере озлокачествления Гомпертца и связаны множеством отношений.
Яков Гельфандбейн
(c) 1011494 CIPO






