Знание порождает, осознание умножает скорбь

Для биоматематиков

Одним из важнейших методов научного познания является математическое моделирование, осуществляемое на моделях, физическая природа которых, отлична от физической природы изучаемого объекта, но сходна с ним в математических отношениях процессов динамики его составляющих. Приемы такого моделирования позволяют, изучая феномен явления, познать скрытное как от прямого, так и непрямого наблюдения, «вещь в себе» - ноумен, делая его «вещью для нас». Познание механизмов динамики озлокачествляющегося клеточного множества можно осуществить путем моделирования систем взаимосвязи и функционального взаимодействия клеточных подмножеств различных состояний, образующих решетку (структуру) - упорядоченное множество, взятое вместе с двумя  бинарными операциями -  объединения и пересечения множеств, при выполнении определенных условий. На решетке клеточных множеств существует отношение решеточного порядка, - она имеет верхнюю и нижнюю границы элементов.

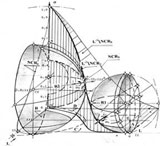На рисунке показано графическое отображение прямой и обратной проекций модели. Ее построение базировалось на решетке клеточных множеств из 10000 элементов на случайных выборках в 2000, 3000, 5000 клеток, полученных в клинике для верифицированных состояний нормального, пластического и гиперпластического эпителия из генеральной совокупности в 50000 клеток, для различных форм и локализации опухолей. Здесь мы дадим краткую обзорную характеристику модели, опишем ее состав и структуру, а затем этапы построения и ее ролевые функции.

Модель представляет собой топологию канонического клеточного множества, на которой определено место каждого из образующих его элементов. Она построена в трехмерной системе координат с центром [1, 1, 0 ] в центре единичного шара, со специфическим (встречным) направлением отсчета независимых переменных (признаков состояния) - ядерно-цитоплазматического отношения (индекса) клеток х и градаций [0,I,II,III,IV] прозрачности L их ядер, определенной так, что  нормированные конечные значения [1] признаков, стремятся к началу координат [1,1,0]. Ордината этой системы r отсчитывается от центра и отображает текущее состояние клетки, нормированное на каноническом состоянии озлокачествления. Таким образом, пространство физической возможности процесса нормировано, и это, с учетом специфики выбранной системы отсчета, определило пространство состояния в правом верхнем сегменте единичного шара. Так как состояние клетки находится в отношении со временем, то одна из координатных плоскостей отображает состояние, другая - редукцию времени канонизации процесса, что придает модели дуальный характер.

Несмотря на явно выраженный размытый характер элементов клеточных подмножеств и их границ, визуально наблюдаемый на клеточном поле, модель носит четкий характер. В ее структуре четко различимы подпространства (подмножества) состояний, объединяющих размытые элементы, образующие эти состояния и разделяющие их поверхности. Это указывает, прежде всего, на реализацию моделью, не только функции разделения состояния клеток по их признакам – поэлементной диагностики, но и выявления отношений между клетками и их множествами - отображения механизмов естественной технологии. Модель обладает свойством четкого структурирования отображений размытых множеств.

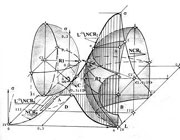
Малая полусфера ограничивает пространство нормального эпителия в системе гомеостазиса – сохранения нормальной жизнедеятельности клеток. Большая полусфера охватывает пространство множества клеток гиперпластического состояния (исключая подмножество «голых» ядер) в системе локального гомеостазиса – сохранения процесса озлокачествления. Подмножество голых ядер, мощностью в 13% клеток, образует точечное множество в близкой окрестности абсолютного фокуса системы r=s, с координатами [1, 1, 1]. Пространства, покрываемые сферами, как и другие пространства модели, носят информационный характер.

Обе полусферы объединены вертикальной линейчатой поверхностью, изгибающейся в сторону абсолютного фокуса – поверхностью перетока. Она образуется на пересечении двух горизонтальных линейчатых поверхностей, образующем линию перетока. Линия перетока отражает фазовую траекторию – след изображающей точки выходной координаты процесса. Выходной координатой процесса является текущее нормированное состояние,  след изображающей точки отражает движение выходной координаты к абсолютному фокусу по минимальному пути за минимальное время. Это свидетельствует о существовании управления технологическим процессом, осуществляющемся по законам оптимального управления, заданного целевой (программирующей) функцией.

Поверхность перетока отображает поверхность раздела двух специфических подпространств. Одно из них, объединят подмножества клеток нормального, инициального (пластического) и канонизируемого (гиперпластического) состояний в баланс эквивалентности, другое в баланс толерантности. Переток клеток во множество, определяющее баланс толерантности, определяет границу функционирования системы гомеостазиса. Множество клеток баланса эквивалентности – резерв клеточных множеств в системе локального гомеостазиса, вовлекаемых в процесс. Множество клеток баланса толерантности – объединяет множество  клеточных подмножеств, вовлеченных в процесс и множество клеток – агрессоров, втягивающих клетки нормального состояния, в  частности - новорожденные, в систему локального гомеостазиса. Поверхность перетока отображает, в пространстве состояний,  локализацию  статистического отношения «левизны-правизны».

Соотношение мощностей этих множеств отражает эффективность управления процессом на редукции времени. В большом числе характерных ситуаций на клеточных множествах, это отношение характеризуется величиной, равной 13 или кратной ей. Инициальное множество клеток пластического состояния, «отрывающееся» от поверхности сферы гомеостазиса, и начинающее движение вдоль линии перетока в направление сферы локального гомеостазиса, в точности соответствует 13% от общего числа клеток эпителиального поля, перетекая ко времени канонизации процесса, в 13% голых ядер, образующих точечное множество  в окрестности фокуса. Значение мощности инициального множества, нормированное на мощности множеств озлокачествленных клеток канонического состояния, определило меру озлокачествления.

Отношения на линейных, площадных и объемных параметрах модели, выраженных на мере озлокачествления, отражают динамику основных инвариантов процесса – констант состояний, множество первичных и вторичных отношений порожденной агрессивности, отражающих переходы от малых количественных изменений признаков в скачкообразные качественные изменения состояний. Некоторые из них, также характеризуются коэффициентами, кратными числу 13. Аналогичную особенность имеют отношения множеств характеристик, отражающих перетоки инвариантов в динамике изменений состояния субстрата. Для проверки этих утверждений, достаточно произвести линейные измерения соответствующих радиусов-векторов, площадей и объмеов на модели, выразив их в единицах меры озлокачествления G.

Проекция прямого сечения единичного шара фазового пространства локального гомеостазиса с системой координат, имеющей  начало в точке 0 - центре шара, позволяет путем геометрических построений, получить некоторый многогранник, в виде замкнутой области  межклеточных взаимодействий множества подмножеств покрываемых им клеток, как непустого связного открытого множества точек топологического пространства порождения и развития древесного роста опухоли. Такой рост отражается в объем единичного, относительно редукции изменения состояния, куба и образует в его объеме характеристическую пирамиду. Верхняя и нижняя грани куба образуются плоскостями IV и 0 градаций L - прозрачности ядер клеток, вырезающими шаровые слои единичного шара, боковые - диаметральными плоскостями шара, играющими роль координатных поверхностей Х - изменения состояния и r - роста.

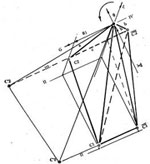Центры шаров гомеостазиса С1 и локального гомеостазиса С2, лежат на одном и том же уровне r озлокачествления, отраженном в значение радиуса шара гомеостазиса R1, но в разных плоскостях - соответственно в плоскости II и III градаций прозрачности ядер. Центры обеих шаров гомеостазиса С1 и локального гомеостазиса С2 и их проекции  и С'1, а также  и С'2 в диаметральных плоскостях соответствующих сфер, соединены между собой и началом 0 системы координат отрезками прямых. Линии, соединяющие центры С1 и С2 шаров и их проекции С'1 и С'2 на собственные верхние полусферы, лежат в первом квадранте единичного шара, в пространстве между плоскостями указанных градаций прозрачности ядер. Линия, соединяющая проекции центров шаров  и  на нижнюю полусферу, проходит в его четвертом квадранте, параллельна линии С1С2 и также пересекают пространство между II и III градациями прозрачности ядер.

В пространстве характеристической пирамиды удобно строить графы на множествах клеточных ситуаций, отражающие парциальность разрастания и сагитальности (стреловидности) множества его направлений, а также трехмерность динамики древесного роста. Использование понятия характеристической пирамиды позволяет формулировать задачи планирования эксперимента в проблеме исследования моделей размножающихся множеств. В этом же пространстве отражается парадокс роста, не получивший своего разъяснения в понятиях используемого подхода.

Установлено также, что отношение объема шара гомеостазиса к объему шара локального гомеостазиса, с достоверностью по вероятности не хуже 1.4% соответствует значению дисплазионной константы (0.3), а обратное отношение, равное 3.33(3)G, соответствует величине радиуса единичного шара, выраженного в единицах G  Гомпертца. Это означает, что расстояние между центрами гомеостазических шаров, обратно пропорциональное значению дисплазионной константы, как и сама константа, есть прогностическое отображение достижимости канонического состояния биологического субстрата, что важно для создания систем ракового скрининга.

Полученные на модели соотношения, позволили отразить порожденные на совершенном строгом порядке клеточных множеств системы гомеостазиса  максимальные совершенные подмножества клеток системы локального гомеостазиса, а также общую упорядоченность функциональных ролей клеточных множеств. Это ставит под сомнение бытующее утверждение о хаотическом росте клеточных множеств опухоли и о потере  клетками, при этом, функциональной дифференцировки. Это же, позволяет утверждать обратное: имеет место строго упорядоченный рост в условиях замены ролевых функций множества подмножеств клеток в системе гомеостазиса, на ролевые функции в системе локального гомеостазиса.

Такой вывод представляется одним их важнейших, определяющих общую стратегию борьбы со злокачественными опухолями. 

Яков Гельфандбейн
© 1011494 CIPO