Тара для сферы

О том, что сфера идеально вписывается в правильный четырехгранник – тетраэдр, – любители стереометрических задачек знают уже почти 400 лет. В 1611 году такое решение предложил великий немецкий астроном и математик Иоганн Кеплер, именем которого, кстати, недавно назван новейший орбитальный телескоп.

Фото: Тара для сферы

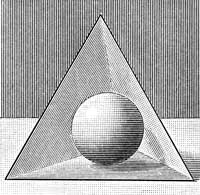
Но сколько всего сфер разного диаметра можно вписать в такую "тару"? Эта задача оказалась сложнее, и вот уже на протяжении более десяти лет ученые из разных стран соревнуются – кто сможет использовать с наибольшей пользой объем тетраэдра.

В 2006 году профессор химии Сальваторе Торквадо и профессор математики Джон Конвэй из Принстонского университета поставили новый мировой рекорд по размещению сфер в тетраэдре. Они смогли заполнить чуть более 72 процентов объема фигуры.

Но год спустя их результат был побит талантливой студенткой Элизабет Чен из Университета Массачусетса. Девушка смогла построить такую компьютерную модель, где было использовано 77,8 процента объема тетраэдра. С этим показателям Чен продержалась в лидерах более двух лет.

И вот новый результат – все тот же Сальваторе Торквадо и аспирант аэрокосмического факультета Принстонского университета Ян Дзяо смогли улучшить предыдущий результат и заполнили 78,2 процента фигуры.

На первый взгляд может показаться, что подобные шарады являются всего лишь своеобразной разминкой для ума, которая не несет никакой практической пользы.

Однако подобное впечатление абсолютно неверно – проблемы компактной и эффективной упаковки касаются самых разнообразных областей человеческой деятельности.

Оставив в стороне логистику, в которой немалую роль играет упаковка перевозимых грузов, стоит обратить внимание на электронику. Именно для решения задач в этом направлении профессор Торквада и занимается поисками решения шарады про сферы и тетраэдр.

Речь идет о технологиях хранения данных. Запись информации на компакт-диски и твердотельные носители очень скоро достигнет электромагнитного предела своего развития, и наука уже давно задается вопросом разработки новых принципов накопления данных.

Ученые предполагают, что, используя все свободные участки магнитных доменов, можно многократно увеличить плотность информации на каждый квадратный миллиметр вещества.

Ян Дзяо, подключившийся к экспериментам профессора Торквады, находит этой шараде другое интересное применение. Дело в том, что в физике экстремально низких температур атомы в кристаллической структуре начинают приближаться друг к другу и стремятся занять как можно меньший объем. Изучение задачи со сферами в тетраэдре позволит спрогнозировать поведение материалов в подобных условиях.

Кроме задач с тетраэдром ученые рассматривают другие правильные трехмерные фигуры, в которые можно упаковать сферы. Внимание математиков привлекают головоломки с кубом, октаэдром (восьмигранник), додекаэдром (двенадцатигранник) и икосаэдром (двадцатигранник), которые также могут оказаться полезными в различных областях физики и материаловедения.